12.2 梯度检查

12.2 梯度检查

12.2.1 为何要做梯度检查？

神经网络算法使用反向传播计算目标函数关于每个参数的梯度，可以看做解析梯度。由于计算过程中涉及到的参数很多，用代码实现的反向传播计算的梯度很容易出现误差，导致最后迭代得到效果很差的参数值。

为了确认代码中反向传播计算的梯度是否正确，可以采用梯度检验（gradient check）的方法。通过计算数值梯度，得到梯度的近似值，然后和反向传播得到的梯度进行比较，若两者相差很小的话则证明反向传播的代码是正确无误的。

12.2.2 数值微分

导数概念回忆

$$\begin{array}{}\text{(1)}& f^{\prime }(x)=\underset{h\to 0}{lim}\frac{f(x+h)-f(x)}{h}\end{array}$$

其含义就是$x$的微小变化$h$（$h$为无限小的值），会导致函数$f(x)$的值有多大变化。在Python中可以这样实现：

def numerical_diff(f, x):
    h = 1e-5
    d = (f(x+h) - f(x))/h
    return d

因为计算机的舍入误差的原因，h不能太小，比如1e-10，会造成计算结果上的误差，所以我们一般用[1e-4,1e-7]之间的数值。

但是如果使用上述方法会有一个问题，如图12-4所示。

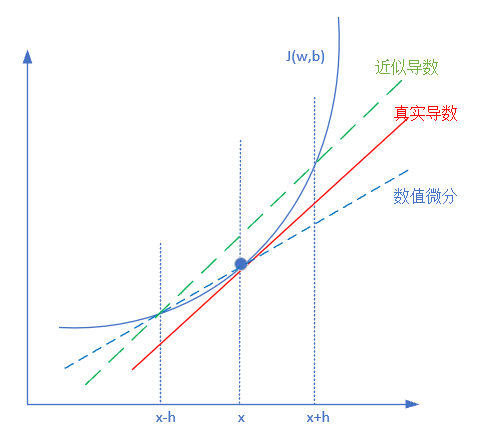
图12-4 数值微分方法

红色实线为真实的导数切线，蓝色虚线是上述方法的体现，即从$x$到$x+h$画一条直线，来模拟真实导数。但是可以明显看出红色实线和蓝色虚线的斜率是不等的。因此我们通常用绿色的虚线来模拟真实导数，公式变为：

$$\begin{array}{}\text{(2)}& f^{\prime }(x)=\underset{h\to 0}{lim}\frac{f(x+h)-f(x-h)}{2h}\end{array}$$

公式2被称为双边逼近方法。

用双边逼近形式会比单边逼近形式的误差小100~10000倍左右，可以用泰勒展开来证明。

泰勒公式

泰勒公式是将一个在$x=x_0$处具有n阶导数的函数$f(x)$利用关于$(x-x_0)$的n次多项式来逼近函数的方法。若函数$f(x)$在包含$x_0$的某个闭区间$[a,b]$上具有n阶导数，且在开区间$(a,b)$上具有$n+1$阶导数，则对闭区间$[a,b]$上任意一点$x$，下式成立：

$$\begin{array}{}\text{(3)}& f(x)=\frac{f(x_0)}{0!}+\frac{f^{\prime }(x_0)}{1!}(x-x_0)+\frac{f^{″}(x_0)}{2!}(x-x_0{)}^2+...+\frac{f^{(n)}(x_0)}{n!}(x-x_0{)}^n+R_n(x)\end{array}$$

其中,$f^{(n)}(x)$表示$f(x)$的$n$阶导数，等号后的多项式称为函数$f(x)$在$x_0$处的泰勒展开式，剩余的$R_n(x)$是泰勒公式的余项，是$(x-x_0{)}^n$的高阶无穷小。

利用泰勒展开公式，令$x=\theta +h,x_0=\theta$，我们可以得到：

$$\begin{array}{}\text{(4)}& f(\theta +h)=f(\theta )+f^{\prime }(\theta )h+O(h^2)\end{array}$$

单边逼近误差

如果用单边逼近，把公式4两边除以$h$后变形：

$$\begin{array}{}\text{(5)}& f^{\prime }(\theta )+O(h)=\frac{f(\theta +h)-f(\theta )}{h}\end{array}$$

公式5已经和公式1的定义非常接近了，只是左侧多出来的第二项，就是逼近的误差，是个$O(h)$级别的误差项。

双边逼近误差

如果用双边逼近，我们用三阶泰勒展开：

令$x=\theta +h,x_0=\theta$，我们可以得到：

$$\begin{array}{}\text{(6)}& f(\theta +h)=f(\theta )+f^{\prime }(\theta )h+f^{″}(\theta )h^2+O(h^3)\end{array}$$

再令$x=\theta -h,x_0=\theta$我们可以得到：

$$\begin{array}{}\text{(7)}& f(\theta -h)=f(\theta )-f^{\prime }(\theta )h+f^{″}(\theta )h^2-O(h^3)\end{array}$$

公式6减去公式7，有：

$$\begin{array}{}\text{(8)}& f(\theta +h)-f(\theta -h)=2f^{\prime }(\theta )h+2O(h^3)\end{array}$$

两边除以$2h$：

$$\begin{array}{}\text{(9)}& f^{\prime }(\theta )+O(h^2)=\frac{f(\theta +h)-f(\theta -h)}{2h}\end{array}$$

公式9中，左侧多出来的第二项，就是双边逼近的误差，是个$O(h^2)$级别的误差项，比公式5中的误差项小很多数量级。

12.2.3 实例说明

公式2就是梯度检查的理论基础。比如一个函数：

$$f(x)=x^2+3x$$

我们看一下它在$x=2$处的数值微分，令$h=0.001$：

$$\begin{array}{}\text{(10)}& \begin{array}{rl}f(x+h)& =f(2+0.001)\\ \\ & =(2+0.001{)}^2+3\times (2+0.001)\\ \\ & =10.007001\end{array}\$\$\$\$\begin{array}{rl}f(x-h)& =f(2-0.001)\\ \\ & =(2-0.001{)}^2+3\times (2-0.001)\\ \\ & =9.993001\end{array}\$\$\$\$\frac{f(x+h)-f(x-h)}{2h}=\frac{10.007001-9.993001}{2\times 0.001}=7\end{array}$$

再看它的数学解析解：

$$\begin{array}{}\text{(11)}& f^{\prime }(x)=2x+3\$\$\$\$f^{\prime }(x{|}_{x=2})=2\times 2+3=7\end{array}$$

可以看到公式10和公式11的结果一致。当然在实际应用中，一般不可能会完全相等，只要两者的误差小于1e-5以下，我们就认为是满足精度要求的。

12.2.4 算法实现

在神经网络中，我们假设使用多分类的交叉熵函数，则其形式为：

$$J(w,b)=-\sum _{i=1}^m\sum _{j=1}^n{y}_{ij}\ln a_{ij}$$

m是样本数，n是分类数。

参数向量化

我们需要检查的是关于$W$和$B$的梯度，而$W$和$B$是若干个矩阵，而不是一个标量，所以在进行梯度检验之前，我们先做好准备工作，那就是把矩阵$W$和$B$向量化，然后把神经网络中所有层的向量化的$W$和$B$连接在一起(concatenate)，成为一个大向量，我们称之为$J(\theta )$，然后对通过back-prop过程得到的W和B求导的结果$d{\theta }_{real}$也做同样的变换，接下来我们就要开始做检验了。

向量化的$W,B$连接以后，统一称作为$\theta$，按顺序用不同下标区分，于是有$J(\theta )$的表达式为：

$$J(w,b)=J({\theta }_1,...,{\theta }_i,...,{\theta }_n)$$

对于上式中的每一个向量，我们依次使用公式2的方式做检查，于是有对第i个向量值的梯度检查公式：

$$\frac{\partial J}{\partial {\theta }_i}=\frac{J({\theta }_1,...,{\theta }_i+h,...,{\theta }_n)-J({\theta }_1,...,{\theta }_i-h,...,{\theta }_n)}{2h}$$

因为我们是要比较两个向量的对应分量的差别，这个可以用对应分量差的平方和的开方（欧氏距离）来刻画。但是我们不希望得到一个具体的刻画差异的值，而是希望得到一个比率，这也便于我们得到一个标准的梯度检验的要求。

为什么这样说呢？其实我们可以这样想，假设刚开始的迭代，参数的梯度很大，而随着不断迭代直至收敛，参数的梯度逐渐趋近于0，即越来越小，这个过程中，分子(欧氏距离)是跟梯度的值有关的，随着迭代次数的增加，也会减小。那在迭代过程中，我们只利用分子就没有一个固定标准去判断梯度检验的效果，而加上一个分母，将梯度的平方和考虑进去，大值比大值，小值比小值，我们就可以得到一个比率，同样也可以得到一个确定的标准去衡量梯度检验的效果。

算法

1. 初始化神经网络的所有矩阵参数（可以使用随机初始化或其它非0的初始化方法）
2. 把所有层的$W,B$都转化成向量，按顺序存放在$\theta$中
3. 随机设置$X$值，最好是归一化之后的值，在[0,1]之间
4. 做一次前向计算，再紧接着做一次反向计算，得到各参数的梯度$d{\theta }_{real}$
5. 把得到的梯度$d{\theta }_{real}$变化成向量形式，其尺寸应该和第2步中的$\theta$相同，且一一对应（$W$对应$dW$, $B$对应$dB$）
6. 对2中的$\theta$向量中的每一个值，做一次双边逼近，得到$d{\theta }_{approx}$
7. 比较$d{\theta }_{real}$和$d{\theta }_{approx}$的值，通过计算两个向量之间的欧式距离：

$$diff=\frac{\parallel d{\theta }_{real}-d{\theta }_{approx}{\parallel }_2}{\parallel d{\theta }_{approx}{\parallel }_2+\parallel d{\theta }_{real}{\parallel }_2}$$

结果判断：

1. $diff>1e^{-2}$

梯度计算肯定出了问题。

1. $1e^{-2}>diff>1e^{-4}$

可能有问题了，需要检查。

1. $1e^{-4}>diff>1e^{-7}$

不光滑的激励函数来说时可以接受的，但是如果使用平滑的激励函数如 tanh nonlinearities and softmax，这个结果还是太高了。

1. $1e^{-7}>diff$

可以喝杯茶庆祝下。

另外要注意的是，随着网络深度的增加会使得误差积累，如果用了10层的网络，得到的相对误差为1e-2那么这个结果也是可以接受的。

12.2.5 注意事项

1. 首先，不要使用梯度检验去训练，即不要使用梯度检验方法去计算梯度，因为这样做太慢了，在训练过程中，我们还是使用backprop去计算参数梯度，而使用梯度检验去调试，去检验backprop的过程是否准确。

2. 其次，如果我们在使用梯度检验过程中发现backprop过程出现了问题，就需要对所有的参数进行计算，以判断造成计算偏差的来源在哪里，它可能是在求解$B$出现问题，也可能是在求解某一层的$W$出现问题，梯度检验可以帮助我们确定发生问题的范围，以帮助我们调试。

3. 别忘了正则化。如果我们添加了二范数正则化，在使用backprop计算参数梯度时，不要忘记梯度的形式已经发生了变化，要记得加上正则化部分，同理，在进行梯度检验时，也要记得目标函数$J$的形式已经发生了变化。

4. 注意，如果我们使用了drop-out正则化，梯度检验就不可用了。为什么呢？因为我们知道drop-out是按照一定的保留概率随机保留一些节点，因为它的随机性，目标函数$J$的形式变得非常不明确，这时我们便无法再用梯度检验去检验backprop。如果非要使用drop-out且又想检验backprop，我们可以先将保留概率设为1，即保留全部节点，然后用梯度检验来检验backprop过程，如果没有问题，我们再改变保留概率的值来应用drop-out。

5. 最后，介绍一种特别少见的情况。在刚开始初始化W和b时，W和b的值都还很小，这时backprop过程没有问题，但随着迭代过程的进行，$W$和$B$的值变得越来越大时，backprop过程可能会出现问题，且可能梯度差距越来越大。要避免这种情况，我们需要多进行几次梯度检验，比如在刚开始初始化权重时进行一次检验，在迭代一段时间之后，再使用梯度检验去验证backprop过程。

代码位置

ch12, Level2

思考与练习

1. 改变任意一行反向传播代码，再运行梯度检查代码，看看结果如何。

0 comments

Anonymous

Error: Not Found.

Markdown is supportedPreviewLogin with GitHub

Be the first person to leave a comment!