10.2 非线性二分类实现

10.2 非线性二分类实现⚓︎

首先定义可以完成非线性二分类的神经网络结构图，如图10-6所示。

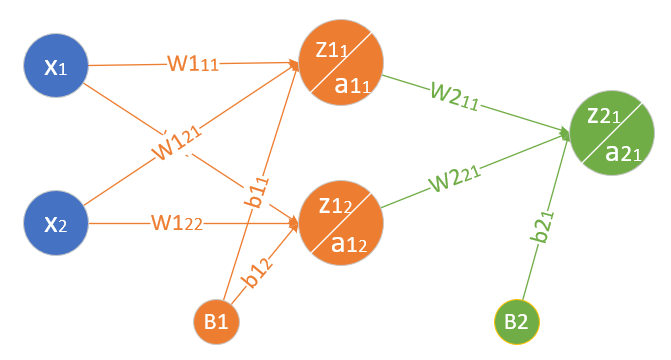
图10-6 非线性二分类神经网络结构图

输入层两个特征值 $x_{1}, x_{2}$ $$ X=\begin{pmatrix} x_1 & x_2 \end{pmatrix} $$
隐层 $2 \times 2$ 的权重矩阵 $W 1$ $$ W1=\begin{pmatrix} w1_{11} & w1_{12} \\ w1_{21} & w1_{22} \end{pmatrix} $$
隐层 $1 \times 2$ 的偏移矩阵 $B 1$

B 1 = (\begin{matrix} b 1_{1} & b 1_{2} \end{matrix})

隐层由两个神经元构成 $$ Z1=\begin{pmatrix} z1_{1} & z1_{2} \end{pmatrix} $$ $$ A1=\begin{pmatrix} a1_{1} & a1_{2} \end{pmatrix} $$
输出层 $2 \times 1$ 的权重矩阵 $W 2$ $$ W2=\begin{pmatrix} w2_{11} \\ w2_{21}
\end{pmatrix} $$
输出层 $1 \times 1$ 的偏移矩阵 $B 2$

B 2 = (\begin{matrix} b 2_{1} \end{matrix})

输出层有一个神经元使用Logistic函数进行分类 $$ Z2=\begin{pmatrix} z2_{1} \end{pmatrix} $$ $$ A2=\begin{pmatrix} a2_{1} \end{pmatrix} $$

对于一般的用于二分类的双层神经网络可以是图10-7的样子。

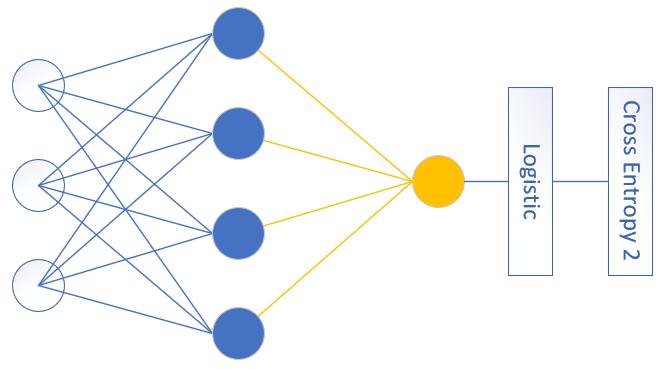
图10-7 通用的二分类神经网络结构图

输入特征值可以有很多，隐层单元也可以有很多，输出单元只有一个，且后面要接Logistic分类函数和二分类交叉熵损失函数。

根据网络结构，我们有了前向计算过程图10-8。

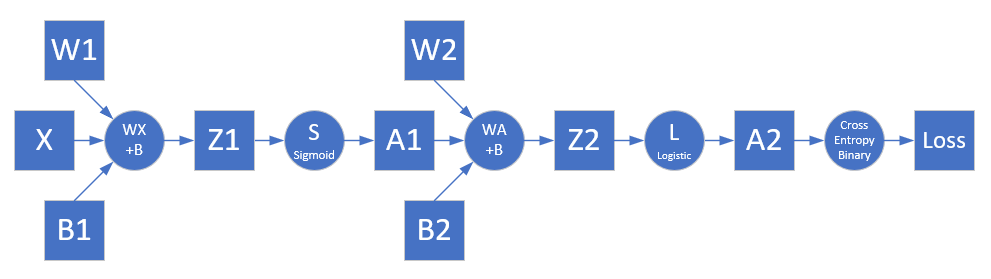
图10-8 前向计算过程

z 1_{1} = x_{1} w 1_{11} + x_{2} w 1_{21} + b 1_{1} $ $ $ $ z 1_{2} = x_{1} w 1_{12} + x_{2} w 1_{22} + b 1_{2} $ $ $ $ Z 1 = X \cdot W 1 + B 1

a 1_{1} = S i g m o i d (z 1_{1}) $ $ $ $ a 1_{2} = S i g m o i d (z 1_{2}) $ $ $ $ A 1 = (\begin{matrix} a 1_{1} & a 1_{2} \end{matrix}) = S i g m o i d (Z 1)

z 2_{1} = a 1_{1} w 2_{11} + a 1_{2} w 2_{21} + b 2_{1} $ $ $ $ Z 2 = A 1 \cdot W 2 + B 2

a 2_{1} = L o g i s t i c (z 2_{1}) $ $ $ $ A 2 = L o g i s t i c (Z 2)

我们把异或问题归类成二分类问题，所以使用二分类交叉熵损失函数：

\begin{matrix} (12) & l o s s = - Y \ln A 2 + (1 - Y) \ln (1 - A 2) \end{matrix}

在二分类问题中， $Y, A 2$ 都是一个单一的数值，而非矩阵，但是为了前后统一，我们可以把它们看作是一个 $1 \times 1$ 的矩阵。

图10-9展示了反向传播的过程。

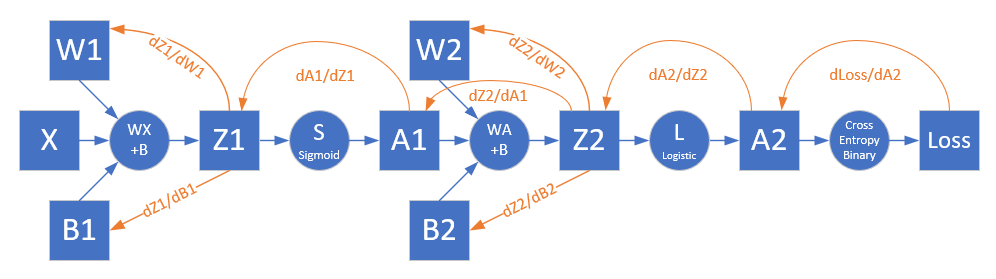
图10-9 反向传播过程

对损失函数求导，可以得到损失函数对输出层的梯度值，即图10-9中的 $Z 2$ 部分。

根据公式12，求 $A 2$ 和 $Z 2$ 的导数（此处 $A 2, Z 2, Y$ 可以看作是标量，以方便求导）：

\begin{matrix} (13) & \begin{aligned} \frac{\partial l o s s}{\partial Z 2} & = \frac{\partial l o s s}{\partial A 2} \frac{\partial A 2}{\partial Z 2} \\ = \frac{A 2 - Y}{A 2 (1 - A 2)} \cdot A 2 (1 - A 2) \\ = A 2 - Y \to d Z 2 \end{aligned} \end{matrix}

Multiple \tag

\begin{matrix} (16) & \begin{aligned} \frac{\partial l o s s}{\partial A 1} & = (\begin{array}{c} \frac{\partial l o s s}{\partial a 1_{1}} & \frac{\partial l o s s}{\partial a 1_{2}} \end{array}) \\ = (\begin{array}{c} \frac{\partial l o s s}{\partial Z 2} \frac{\partial Z 2}{\partial a 1_{1}} & \frac{\partial l o s s}{\partial Z 2} \frac{\partial Z 2}{\partial a 1_{2}} \end{array}) \\ = (\begin{array}{c} d Z 2 \cdot w 2_{11} & d Z 2 \cdot w 2_{21} \end{array}) \\ = d Z 2 \cdot (\begin{array}{c} w 2_{11} & w 2_{21} \end{array}) \\ = d Z 2 \cdot W 2^{⊤} \end{aligned} \end{matrix}

\begin{matrix} (17) & \frac{\partial A 1}{\partial Z 1} = A 1 ⊙ (1 - A 1) \to d A 1 \end{matrix}

所以最后到达 $Z 1$ 的误差矩阵是：

\begin{matrix} (18) & \begin{aligned} \frac{\partial l o s s}{\partial Z 1} & = \frac{\partial l o s s}{\partial A 1} \frac{\partial A 1}{\partial Z 1} \\ = d Z 2 \cdot W 2^{⊤} ⊙ d A 1 \to d Z 1 \end{aligned} \end{matrix}

有了 $d Z 1$ 后，再向前求 $W 1$ 和 $B 1$ 的误差，就和第5章中一样了，我们直接列在下面：

Multiple \tag